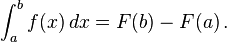My module

Introduction 1
Intergartion is revised differentiation 2
Integrsation 3
Animation 4
Aktivity sheet
Lesson Plan

1.

2.

3.

Integral

From Wikipedia, the free encyclopedia

Topics in calculus

Fundamental theorem Limits of functions Continuity Vector calculus Matrix calculus Mean value theorem

Differentiation

Product rule Quotient rule Chain rule Change of variables Implicit differentiation Taylor's theorem Related rates List of differentiation identities

Integration

Lists of integrals Improper integrals Integration by: parts, disks, cylindrical shells, substitution, trigonometric substitution, partial fractions, changing order

A definite integral of a function can be represented as the signed area of the region bounded by its graph.

Integration is an important concept in mathematics, specifically in the field of calculus and, more broadly, mathematical analysis. Given a function ƒ of a real variable x and an interval [a,b] of the real line, the integral

is defined informally to be the signed area of the region in the xy-plane bounded by the graph of ƒ, the x-axis, and the vertical lines x = a and x = b.

The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function f. In this case it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antiderivatives and indefinite integrals.

The principles of integration were formulated independently by Isaac Newton and Gottfried Leibniz in the late seventeenth century. Through the fundamental theorem of calculus, which they independently developed, integration is connected with differentiation: if f is a continuous real-valued function defined on a closed interval [a, b], then, once an antiderivative F of f is known, the definite integral of f over that interval is given by

Integrals and derivatives became the basic tools of calculus, with numerous applications in science and engineering. A rigorous mathematical definition of the integral was given by Bernhard Riemann. It is based on a limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs. Beginning in the nineteenth century, more sophisticated notions of integral began to appear, where the type of the function as well as the domain over which the integration is performed has been generalised.